Cryptoverse CTF 2023
On CTFtime

There are many challenges in this CTF which are great for learning yet still challenging and not trivial. Kudos to the organiser! Here are the writeups to some of the challenges my team solved.

On this page:

Crypto Warmup 1

Decode the following ciphertext: GmvfHt8Kvq16282R6ej3o4A9Pp6MsN.

This actually took my team a while to figure out, and this challenge got fewer solves compared to Crypto Warmup 2 below (175 and 233 solves respectively). Turns out to solve it need to do rot13 then base58 decode.

The flag is cvctf{base58_with_rot}.

Crypto Warmup 2

This cipher is invented by French cryptographer Felix Delastelle at the end of the 19th century.
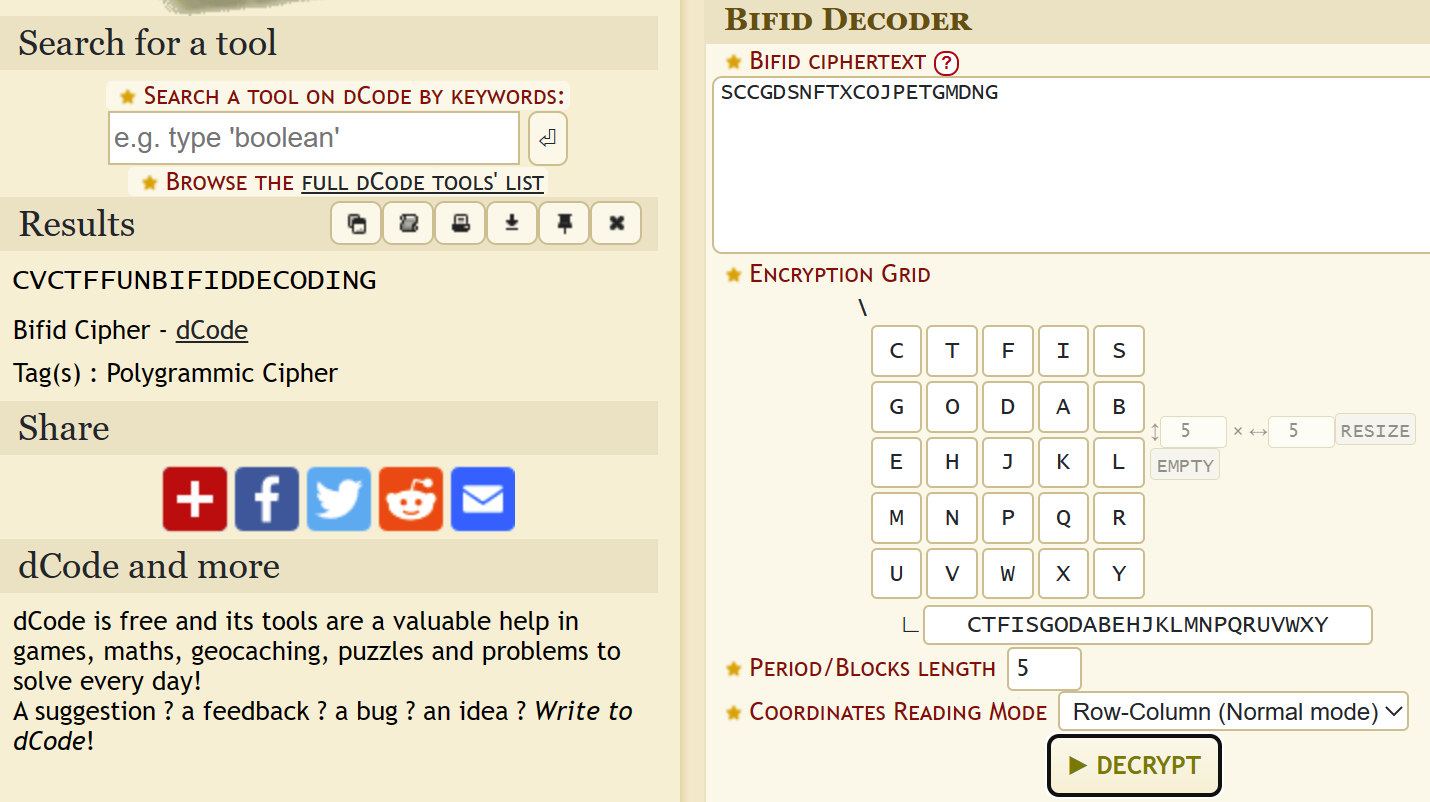
Ciphertext: SCCGDSNFTXCOJPETGMDNG Hint: CTFISGODABEHJKLMNPQRUVWXY

When seeing random ciphers in CTF, I immediately think of dcode.fr. After a quick Google search for “Felix Delastelle cipher”, the 3rd result was the link to decode.fr.

Bifid decoder

Crypto Baby AES

In this challenge the flag is encrypted with AES CBC mode, with IV and the encrypted flag provided in the output. The key is generated with the code below:

KEY_LEN = 2
BS = 16
key = pad(open("/dev/urandom","rb").read(KEY_LEN), BS)

The unknown part of the key is only 2 bytes, so we can brute force it, and decrypt the flag.

Misc Minecraft’s Deadly Dilemma

The challenge provided two grayscale images “pickaxe.png” and “sword.png”, and the goal is to find a image with L1 distance to “pickaxe.png” close enough that is smaller than , but with L2 distance to “pickaxe.png” larger than to “sword.png”. The L2 distance between the provided two images is 10411.40 and the L1 distance is 442888.

To find such image, I tried two approaches:

  • The first one is to start with “pickaxe.png”, so the L1 distance is 0, and then change the pixels value where “pickaxe.png” is smaller than “sword.png” to the maximum value, which would result in a larger increase in L2 distance for “pickaxe.png” than for “sword.png” until before the L1 distance reaches over 224676. However, as the L2 distance to “sword.png” is already quite large, the L1 distance would reach over 474 before the L2 distance to “pickaxe.png” is larger than to “sword.png”.

  • The second approach is also to start with “pickaxe.png”, but instead of increasing the L2 distance for “pickaxe.png”, I reduce the L2 distance to “sword.png” while increasing the L2 distance to “pickaxe.png” until the L2 distance to “pickaxe.png” is larger than to “sword.png” while the L1 distance is still smaller than 224676. The code is shown below:

    xy = []
for i in range(64):
  for j in range(64):
      p1 = pick.getpixel((i, j))
      p2 = sword.getpixel((i, j))
      xy.append((p1 - p2, (i, j)))
xy.sort() # large negative first
for i in range(3500):
  p, c = xy[i]
  pick.putpixel(c, sword.getpixel(c))
pick.save('out.png')

Reverse Simple Checkin

Decompile the binary provided with the binary, realising the binary is to check if the input xor with some data is equal to some other data. Implemented the script in Python to xor the two data and get the very long flag:

cvctf{i_apologize_for_such_a_long_string_in_this_checkin_challenge,but_it_might_be_a_good_time_to_learn_about_automating_this_process?You_might_need_to_do_it_because_here_is_a_painful_hex:32a16b3a7eef8de1263812.Enjoy(or_not)!}

Reverse Micro Assembly

In this challenge, an assembly file in AT&T syntax is provided. After Googling around of the instructions (especially something special with the DIV instruction which takes 3 arguments and followed with instruction to compare value in register 12), I found out that the assembly is “hypothetical assembly language”, which is based on x86 assembly. The instructions reference can be found on http://www.ctoassembly.com/asm.html.

As there are conditional jumps in the assembly, however they do not form any loops, I solved this challenge by hand and the resulting stack contains the flag.

Reverse Solid Reverse

This challenge is to reverse a smart contract in Solidity. The contract is shown below:

contract ReverseMe {
    uint goal = 0x57e4e375661c72654c31645f78455d19;
    function magic1(uint x, uint n) public pure returns (uint) {
        // Something magic
        uint m = (1 << n) - 1;
        return x & m;
    }
    function magic2(uint x) public pure returns (uint) {
        // Something else magic
        uint i = 0;
        while ((x >>= 1) > 0) {
            i += 1;
        }
        return i;
    }
    function checkflag(bytes16 flag, bytes16 y) public view returns (bool) {
        return (uint128(flag) ^ uint128(y) == goal);
    }
    modifier checker(bytes16 key) {
        require(bytes8(key) == 0x3492800100670155, "Wrong key!");
        require(uint64(uint128(key)) == uint32(uint128(key)), "Wrong key!");
        require(magic1(uint128(key), 16) == 0x1964, "Wrong key!");
        require(magic2(uint64(uint128(key))) == 16, "Wrong key!");
        _;
    }
    function unlock(bytes16 key, bytes16 flag) public view checker(key) {
        // Main function
        require(checkflag(flag, key), "Flag is wrong!");
    }
}

The unlock function will check if the key is correct through the checker modifier. Then it will check that the flag xor with the key is equal to the goal. So we can get the flag by xor the goal with the key. The key is not provided, but we can get it by solving the checker modifier.

The magic1 function is to get the lower 16 bits of the key, and the magic2 function is to get the number of bits of the key.

  • The first line of the checker is to check if the first 8 bytes of the key is 0x3492800100670155.
  • The second line is to check that the lower 32 bits of the key is equal to the lower 64 bits of the key, which means the upper 32 bits in the lower 64 bits of the key is zero.
  • The third line is to check that the lower 16 bits of the key is 0x1964.
  • The fourth line is to check that the number of bits of the lower 64 bit of the key is 16 + 1 = 17 excluding leading zeros. This resulting in the lower 64 bit of the key is between 0x10000 and 0x1ffff.

The final key is 0x34928001006701550000000000011964, and flag can be obtained by xor the key with the goal.

Pwn Acceptance

The challenge provided a binary executable. Decompile the binary with IDA, the code snip for main function is shown below:

read(0, &say, 0x24uLL);
if ( accept )
  print_flag();
else
  puts("Arg! Why don't you help me :((");
return 0;

Looking into &say, it points to some statically allocated variable (.bss) with size of 32 bytes, while the read would read up to 0x24 (36) bytes. The accept variable is 4 bytes and is located right after &say. So we can overflow the accept variable and overwrite it with non-zero value to make print_flag() to be called.

Decompile the print_flag() function, there are two condition checks before the flag is actually printed. The first one is to check if the accept variable is smaller or equal to 0, the second one is to check if the accept variable is equal to -1.

To solve the challenge, I send 32 bytes of arbitrary data, followed by -1 encoded for 4 bytes, which is \xff\xff\xff\xff. The flag is printed out.

from pwn import *
p = remote('example.com', 4000)
p.recvuntil(b'Help him: ')
payload = b'a' * 32 + b'\xFF\xFF\xFF\xFF'
p.sendline(payload)
p.interactive()

Web Safe Locker

The goal of the challenge is to find the passcode.

Safe locker page

The relevant code is within a JavaScript module on this page. The actual check appears to be done with web assembly. However, without reversing the web assembly, I can still bruteforce the passcode with the JavaScript code. There are only 10,000,000 possible passcodes, and it is possible to bruteforce, however the web page crashes if I try to bruteforce all the passcodes at once. So I bruteforce the passcode in batches, also this allows me to do them parallelly in different browser tabs.

import('/passCheck.js').then(m => m.default()).then(m => password_checker = m.cwrap('checker', 'boolean', ['string']))
for (const p of Array(10000000).keys()) {
    let s = '00000000' + (p + 10000000);
    s = s.substr(s.length - 8)
    if (password_checker(s, 8)) {
        console.log(s);
    }
}

This is also another not bruteforcable version of this challenge in the CTF, which checks an extra string value. I have not tried to solve it yet.

HoYoverse II: Prompt Bot

In this challenge, the goal is to send prompt (there is a character limit of the prompt length, so the prompt cannot be too long. Also the prompt cannot contain the exact target) that makes the ChatGPT bot to output the exact target response.

The targets are:

  • dlrow olleh
  • zellic zelli zell zel ze z
  • *****
****
***
**
*

My prompts are:

  • reverse hello world
  • zellic zelli zell zel ze Z to lower
  • 5 lines of *, with 5 to 1

I got the 2nd prompt inspiration from my teammate’s screenshot, where the output he got with all Zs in upper case. So I tried to make the Z in lower case, and it worked.

Screenshot of the response my teammate got

HoYoverse III: Secret Vault

This challenge is with a provided Python file, the snip of the code is shown below:

from secret import FLAG
FLAG = FLAG[6:-1]
class HoYoVault:
    def __init__(self, u, v, w):
        self.state = [u, v, w]
        while True:
            self.p = getPrime(64)
            self.a = bytes_to_long(FLAG[:6])
            self.b = bytes_to_long(FLAG[6:12])
            self.c = bytes_to_long(FLAG[12:18])
            self.d = bytes_to_long(FLAG[18:])
            if self.p > max([self.a, self.b, self.c, self.d]):
                break
    def Generate(self):
        data = (self.a * self.state[-1] + self.b * self.state[-2] + self.c * self.state[-3] + self.d) % self.p
        self.state.append(data)
        return data
def main():
    vault = HoYoVault(getRandomInteger(128), getRandomInteger(256), getRandomInteger(512))
    print("data = " + str([vault.Generate() for _ in range(7)]))
    print("p = " + str(vault.p))
if __name__ == "__main__":
    main() 
# data = [14169084828739113416, 12950362233651727953, 13081576751296291893, 11189892724250189745, 2366046383900978737, 1749792629103627315, 8575562236709928474]
# p = 16200480981168924301

From the code, I can see the outputted data is generated through the flag and previous states, while the generated data is appended to state to be used in generating future data.

With enough data output provided, I can form a system of linear equations, and solve for the flag.

data = [14169084828739113416, 12950362233651727953, 13081576751296291893, 11189892724250189745, 2366046383900978737, 1749792629103627315, 8575562236709928474]
# modified from code from https://stackoverflow.com/a/62600438
import sympy
eq = []
values = []
for i in range(len(data) - 3):
    eq.append([data[i], data[i + 1], data[i + 2], 1])
    values.append(data[i + 3])
eq = sympy.Matrix(eq)
values = sympy.Matrix(values)
m = 16200480981168924301
det = int(eq.det())
if gcd(det, m) == 1:
    ans = int(pow(det, -1, m)) * eq.adjugate() @ values % m
flag = b''
for i in ans:
    flag += int(i).to_bytes(6, 'big')
print(flag)

I was also trying to use solve_mod in SageMath instead of pulling code from Stack Overflow, which worked great in one of the ImaginaryCTF challenges sharing the very similar idea but with an a lot smaller modulus. However, when I used it in this challenge, I got the following error:

OverflowError: Python int too large to convert to C ssize_t

After the CTF ended, on Cryptoverse Discord server, Neobeo from the “Social Engineering Experts” team (I think) suggested that they were able to define the linear equations in a Finite Field in SageMath and used solve_right to solve the equations.